
푸는데 3일 걸렸고요. 진짜 너무너무 괴로웠고요...
맨날 실버 풀다가 오랜만에 플레 함 해볼까 했다가 대가리 시원하게 박살났음니다.
다시는 플레를 조심성 없이 고르지 않으리...
푸념은 여기까지 하고, 아래는 문제입니다.

영화로 10만 개로 젠가 하는 미친놈이 너 말고 또 있을까 상근아?
죄송합니다. 문제 볼게요.
사실 문제 유형 파악부터 굉장히 애먹었습니다. 이분 탐색인가? 하니 정렬 데이터가 아니고, 그리디인가? 하니 모든 비용이 1입니다. 최단 거리, 최소 비용 알고리즘인가? 하면 사실 적용법이 떠오르지 않았고요... 설마 트리겠어? 했는데 아니나 다를까 트리였습니다. 그것도 딱 한 번 해봤던 세그먼트 트리요...
세그먼트 트리는 구간 정보를 다룰 때 유리한 자료구조입니다. 일반적으로 구간 합, 구간 최소/최대 값을 다룰 때 사용할 수 있습니다. 저도 써보는 건 이번이 두 번째라 자세힌 모르겠지만, 구간 별로 일관되게 추출할 수 있는 값이 있다면 사용할 수 있는 느낌입니다. 이번엔 구간합을 이용해서 상근이의 괴랄한 영화 감상을 알아볼 겁니다.

대가리가 나쁜 상근이는 영화를 이렇게 쌓아둔 것 같습니다. 우리가 할 일은 꺼내야 할 영화 위에 다른 영화가 몇 개나 있는지 찾는 겁니다. 중간 값 하나를 빼서 계속 위로 쌓아주면 된다는 걸 생각하면 앞, 뒤로 데이터를 삽입하는 큐나 스택이 떠오르기도 합니다.
문제는 데이터의 범위입니다. 영화의 개수와 최대 탐색 횟수가 모두 10만으로, 찾고 꺼내서 삽입하는의 과정이 최악의 경우 10만 x 10만으로 100억 번의 연산이 필요해집니다. 뒤의 탐색 횟수는 문제에서 주어지는 것이기 때문에 우리가 컨트롤할 수 없습니다. 따라서 문제 풀이를 위해선 10만 개의 데이터 중 원하는 값을 찾는 탐색 시간을 줄여야 한다는 결론을 내릴 수 있습니다. 검색에 O(n)의 시간복잡도가 필요한 자료구조를 제외하고, 키워드는 '탐색' 혹은 원하는 조건의 데이터를 찾는 '검색'이라고 한다면 트리를 사용하면 좋겠다고 연결할 수 있겠습니다.
지금부턴 편의상 그림을 가로로 돌려서 보겠습니다.

처음 영화의 상태입니다. 1 - 8까지 순서대로 꽂혀있죠. 예 꽂혀있습니다. 가로로 놓으면 이렇게 편한 걸 상근이 빡대가리는 왜 세로로 올려서 개수를 세고 젠가를 하고 있을까요... 여하튼...
6번 영화를 위로 올리는 상황을 가정해 봅시다.

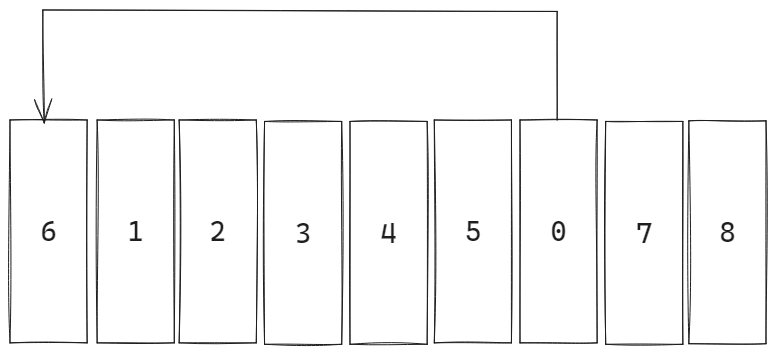
빈 공간을 0이라고 하면 진행은 위와 같습니다. 사실 뻔한 진행이니, 한 번 정도만 더 그림으로 보겠습니다.


이번엔 2를 위로 올려봤습니다. 역시 빈 공간은 0입니다. 우리가 필요한 건 영화의 개수입니다. 위에 몇 번 영화가 있는지가 중요한 게 아니라, 단순히 영화가 있다, 없다만 판단하면 됩니다. 위 그림을 조금 바꿔서, 영화가 있는 곳을 1, 없는 곳을 0으로 표현해 보겠습니다.

이번엔 1번 영화를 선택했습니다. 1로 표시된 영화 두 개를 넘어 앞쪽으로 이동합니다. 이때 노란색으로 표시된 구간의 합이 위에 있는 영화의 개수가 됩니다. 한 번의 이동만 더 해보겠습니다.

이번엔 3번 영화(헷갈린다면 첫 이미지 참고)를 가장 앞으로 옮겼습니다. 이때 3번 위에 있는 블록은 모두 5개이지만, 1로 표시된 구간만 더하기 때문에 3번 위에 있는 영화의 개수는 3개가 됩니다.
즉 영화가 있는 칸을 1, 비워진 곳을 0으로 채우고 목표 영화의 위치까지 구간 합을 구하다 보면 정답을 도출할 수 있습니다.
구간합 = 세그먼트 트리 활용까지는 익숙하니 이제 문제를 풀기 위해 어떻게 트리를 구성할지 생각해 보겠습니다. 제가 이해한 바로는 세그먼트 트리는 첫 빌드 후 크기가 정적입니다. 그러나 문제에선 영화의 위치가 바뀔 때마다 인덱스가 하나씩 늘어나고 있습니다.
저는 이 부분 때문에 정말 오랜 시간 고민했는데 답은 문제에 있었습니다. 영화를 몇 번 선택할지 문제에서 변수 m을 쥐어주기 때문에, 우리는 트리를 만들 때 이동에 필요한 공간을 미리 할당해서 사용할 수 있습니다. 원래 트리를 구성할 때 변수 n으로 공간을 할당했다면, 이동할 영화가 들어갈 위치까지 더해서 n+m으로 트리를 구성하는 것이죠.
세그먼트 트리를 구현하는 방법은 후에 포스팅을 추가하도록 하겠습니다. 오늘 모든 걸 다 적기엔 나 너무 힘드뤄...
라고하고 싶은데 사실 그것보다는 제 이해가 좀 더 올라온 후에 포스팅하는 게 맞을 것 같아서요. 아래는 문제 풀이입니다.
예제 1번의 첫 번째 테스트 케이스를 기준으로 세그먼트 트리를 그려보겠습니다.
데이터는 영화 1, 2, 3
선택 영화는 3, 1, 1 순입니다.

트리를 구성했을 때 최초 상태입니다. n과 m이 각각 3으로 주어졌고, 올릴 영화의 위치를 앞에 3칸, 이미 존재하는 영화의 위치를 뒤쪽 3칸으로 구성했습니다. 루트 노드의 좌 우로 1-3, 4-6 위치의 공간이 할당된 모습입니다. 최상단으로 옮겨지는 영화의 위치를 기억하기 위해 배열을 하나 생성해 둡니다. 각 영화가 몇 번째 공간으로(몇 번째 순서로) 선택되었는지 저장하고 구간합의 범위를 계산할 때 사용합니다..

첫 번째 영화인 3번을 선택했을 때의 변화를 보겠습니다. 이때 정답에 추가되는 값은 빈칸 3 + 3(영화의 위치) 범위의 구간합 -1(본인을 제외하고 카운트해야 하므로)이 됩니다. 쿼리로 생각하면 1~6까지의 합에서 1을 뺀 값이라고 할 수 있습니다. 정답에 값 2가 추가됩니다. 아래는 업데이트 후의 트리입니다.

3번 영화 자리에 채워진 1을 0으로 업데이트하고, 비워뒀던 앞 3칸 중 3번째 칸에 1을 업데이트한 모습입니다.

상태 저장 배열에서 3번 영화의 값이 업데이트됩니다. 3번 영화가 3번째 칸 (총 3번의 선택 중 첫 번째)에 옮겨졌으므로 위와 같이 기록됩니다.
이제 두 번째 영화 선택을 진행하겠습니다. 1번 영화를 선택하고 트리를 업데이트합니다. 이번엔 1 - 4(3칸 + 1번 영화의 위치) 구간의 구간합에서 -1한 값인 1이 정답에 추가됩니다.

1번 영화가 있던 자리가 0으로 업데이트되고 비워놨던 2번째 칸에 1을 업데이트 합니다.

1번 영화가 2번 칸에 업데이트되고 기록됩니다.
이제 마지막으로 1번 영화를 선택합니다. 위에서 1이 2번 칸으로 업데이트되었다고 기록되어 있기 때문에 이번엔 1부터 2까지의 구간합 -1인 0을 정답에 업데이트합니다.

트리는 위와 같이 업데이트되고

상태 배열은 1을 1에 채웠기 때문에 위와 같은 상태로 마무리됩니다.
정답 배열은 그림이 없어서 되려 보기가 어려운데, 각 선택마다 볼드채로 표기되어 있습니다. 최종적으로 정답은 2,1,0이 됩니다.
아래는 파이썬으로 구현한 코드입니다.
# BOJ 3653 영화 수집
import sys
input = sys.stdin.readline
def get_input():
n, m = list(map(int, input().split()))
movies = list(map(int, input().split()))
return [n, m, movies]
def solution(params):
# 트리 빌드
def set_tree(index, left, right):
if left == right:
tree[index] = 0 if left <= m else 1
return tree[index]
mid = (left + right) // 2
tree[index] = set_tree(index * 2, left, mid) + set_tree(
index * 2 + 1, mid + 1, right
)
return tree[index]
# 노드의 인덱스, 노트 시작 범위, 노드 끝 범위, 탐색 시작 범위, 탐색 끝 범위
def get_sum(index, start, end, left, right):
# 현재 노드가 탐색 구간을 포함하지 않으면
if end < left or start > right:
return 0
# 현재 노드가 탐색 구간을 완전히 포함하면
elif left <= start and right >= end:
return tree[index]
mid = (start + end) // 2
return get_sum(index * 2, start, mid, left, right) + get_sum(
index * 2 + 1, mid + 1, end, left, right
)
# 노드의 값을 업데이트 합니다
def update(index, start, end, target, value):
if start > target or end < target:
return
tree[index] += value
if start == end:
return
mid = (start + end) // 2
update(index * 2, start, mid, target, value)
update(index * 2 + 1, mid + 1, end, target, value)
n, m, selected = params
answer = []
# 테스트 케이스마다 선택된 영화를 저장해준다
record = [-1 for _ in range(n + 1)]
tree = [0 for _ in range(4 * (n + m))]
# 트리를 초기화 해준다
# m칸을 비우고!
set_tree(1, 1, m + n)
# 로직 실행
for i, cur in enumerate(selected):
# 0부터 시작하니 -1
# record 배열에 저장된 값이 없다면 원래 순서까지 구간합
target = cur + m if record[cur] == -1 else record[cur]
# 구간합 계산
value = get_sum(1, 1, n + m, 1, target)
# 구간합 -1을 정답에 추가
answer.append(value - 1)
# 선택 영화의 원래 위치는 0으로 업데이트
update(1, 1, n + m, target, -1)
# 선택 영화를 새로운 칸에 1로 업데이트
update(1, 1, n + m, m - i, 1)
# 선택 영화 위치 기록 남기기
record[cur] = m - i
return answer
if __name__ == "__main__":
T = int(input())
answer = []
for _ in range(T):
answer.append(solution(get_input()))
for a in answer:
print(*a)
'Algorithm > 문제 풀이' 카테고리의 다른 글
| 프로그래머스 - 봉인된 주문 (0) | 2025.02.19 |
|---|---|
| BOJ 11726 - 2 x n 타일링 (0) | 2024.06.17 |
| BOJ 11834 - 홀짝 (0) | 2024.06.09 |
| BOJ 10868 - 최솟값 (0) | 2024.06.04 |
| BOJ 3080 - 아름다운 이름 [Java / Python] (0) | 2024.06.02 |



