
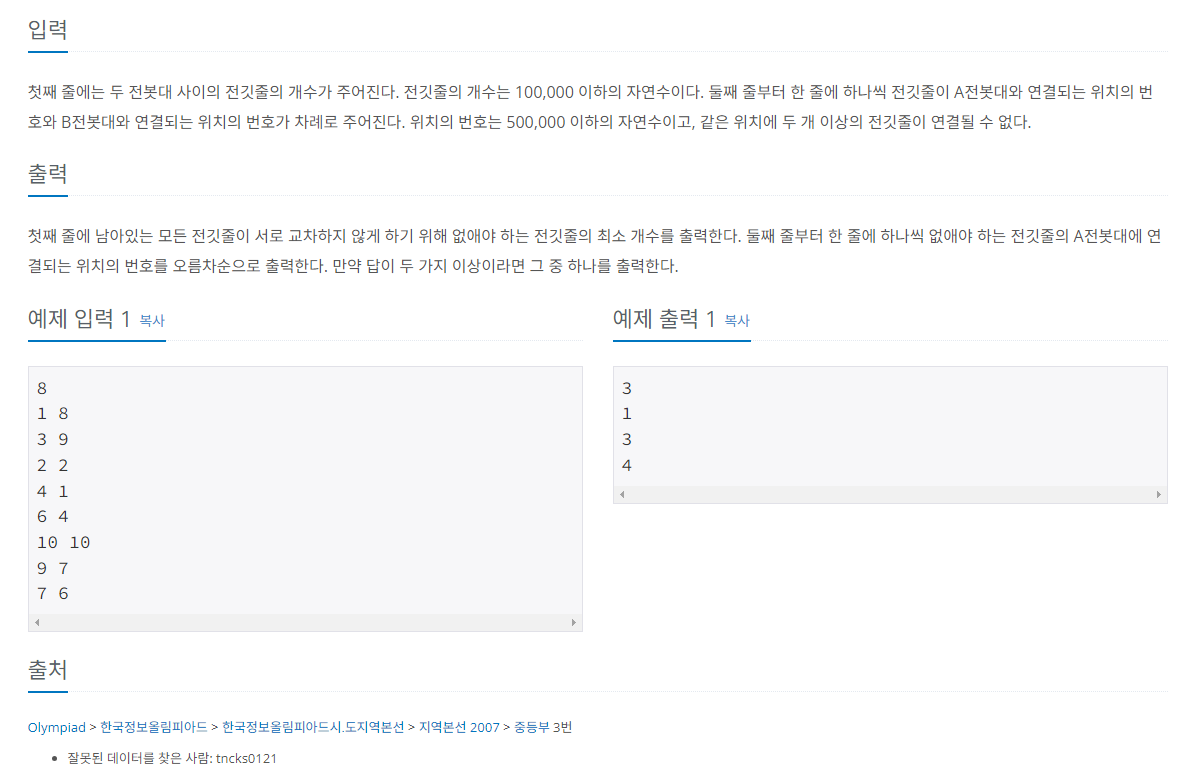
이름이 재밌어 보여서 골랐는데, 직전에 풀었던 BOJ 12015 가장 긴 증가하는 부분 수열과 동일한 문제다. A의 번호를 index, B를 value로 생각하면 이 문제와 동일한 방법으로 남겨야 할 줄의 개수를 찾을 수 있다.
BOJ 12015 - 가장 긴 증가하는 부분 수열 2
단계별 풀어보기 DP단락에 있는 BOJ 11053 - 가장 긴 증가하는 부분 수열과 동일한 문제입니다.다만 입력값의 범위가 크게 늘어난 만큼, 풀이 방법에 개선이 필요합니다. 먼저 입력이 1 인 BOJ 11053의
dooduz.tistory.com
그러나 이번에는 길이만 구하는 게 아니라, 몇 번 줄을 잘라냈는지 함께 보여줘야 한다. 기존 방법에선 index에 상관없이 dp[n]의 길이별 최소값을 저장했는데, 이번엔 해당 인덱스에서 가질 수 있는 LIS(Longest Increasing Subsequence)길이를 저장하는 배열을 함께 사용할 것이다.
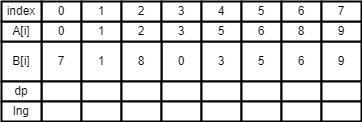
예제의 초기 배열이다. A[i]와 B[i]의 값은 문제 풀이 코드에 맞춰 0-index로 표현했다. dp갱신에 대한 설명은 위 링크에 나와있으니, 이번엔 lng 배열 갱신에 초점을 맞춰 진행해 보겠다.

index = 1까지 진행한 모습이다. [ 7, 1 ]은 LIS가 될 수 없으므로 dp[0]은 7에서 1로 갱신됐다. 그러나 lng 배열은 그대로 1로 유지된다. index = 1일 때 가질 수 있는 최대 LIS가 1이기 때문이다. 당장 이게 무슨 상관인가 싶더라도 뒤의 과정을 더 진행해 보자.

index = 2까지 진행했을 때 dp[1]값은 8로, lng[2] 값은 2로 갱신됐다. 해당 위치의 값을 포함했을 때 가질 수 있는 LIS 최대 값은 [ 1, 8 ] 혹은 [ 7, 8 ]로 2이기 때문이다.
index = 3이 중요하다. B[i] = 0이므로 dp[0]의 값이 1에서 0으로 갱신되는데, lng[3]의 값은 되려 1로 감소했다. dp는 LIS값을 찾기 위해 사용하는 'LIS 길이 별 최소값'을 저장하기 때문에 index에 상관없이 값을 갱신하지만, lng은 해당 index 값을 포함했을 때 가질 수 있는 LIS값이기 때문에 그렇다. B[3] = 0이기 때문에 dp[n]에서 n = 0인 자리, 즉 길이가 1일 때의 최소값 자리에 저장됐으므로 lng[3] = 1일 수밖에 없다. [ 7, 1, 8, 9 ] 중 어느 것도 0보다 작지 않기 때문이다.

index = 4까지 진행했을 때 dp[1] = 3 으로 갱신된다. lng[4] 역시 B[4] = 3의 값이 dp[n]에서 n = 1자리에 갱신 됐으므로, B[4]를 사용했을 때 가질 수 있는 LIS는 n+1인 2다.
index = 5 일 때도 동일하다. B[5] = 5이므로 dp[2]자리에 갱신되고, lng[5]는 3으로 갱신된다.
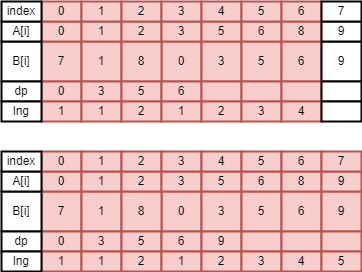
동일하게 마지막까지 진행했다. 이렇게 하면 LIS의 길이를 구할 수 있을 뿐만 아니라, lng배열에 기록한 길이를 역추적해 LIS 배열까지 얻을 수 있다.
위 이미지 대로 lng = 5인 부분부터 lng = 1인 부분까지 A[i]를 역추적하면, 문제에서 요구하는 LIS를 찾을 수 있다.
A의 3, 5, 6, 8, 9에서 출발하는 줄을 남겨두고 1,2,3을 자르는 식이다. 예제 출력과 값이 달라도 괜찮다! 답이 여러 개 이상일 수 있는 문제이고, 위 답은 문제 조건에 부합한다.
구현 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.StringTokenizer;
public class Main {
static int N;
static int[][] arr;
static int[] dp;
static int[] lng;
static int idx = 0;
public static void main(String[] args) {
try {
input();
} catch (IOException e) {
e.printStackTrace();
}
StringBuilder sb = new StringBuilder();
for (int i = 1; i < N; i++) {
if (arr[i][1] > dp[idx]) {
idx++;
dp[idx] = arr[i][1];
lng[i] = idx;
} else {
int l = 0;
int r = idx;
int mid;
while (l < r) {
mid = (l + r) / 2;
if (dp[mid] < arr[i][1]) {
l = mid + 1;
} else {
r = mid;
}
}
dp[r] = arr[i][1];
lng[i] = r;
}
}
// N에서 남은 줄 수를 차감 = 제거한 줄의 수
sb.append(N - (idx + 1));
for (int i = lng.length - 1; i >= 0; i--) {
if(lng[i]==idx){
idx--;
}else {
sb.append('\n');
sb.append(arr[i][0]);
}
}
System.out.println(sb);
}
static void input() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
arr = new int[N][2];
dp = new int[N];
lng = new int[N];
StringTokenizer st;
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
arr[i] = new int[]{a, b};
}
Arrays.sort(arr, (e1, e2) -> {
return e1[0] - e2[0];
});
// 출발 값 초기화
dp[0] = arr[0][0];
dp[0] = arr[0][1];
}
}

사실 평소라면 못 풀었을 문제인데, 어제 풀었던 문제와 공교롭게도 같은 유형의 문제라 접근이 가능했다.
솔직히 말하면 같은 유형의 문제인 걸 알고도 어떤 전깃줄을 잘라야 하는지 판단하는데 한참 걸렸다.
운이 한참 좋았던 나... 라고 할 수 있겠다.
오늘은 위상 정렬 문제를 하나 더 풀었는데, 오늘 푼 두 문제 모두 답이 여러 개일 수 있는 것도 묘하다.
아 그리고... 필자는 문제풀이에 0-index를 쓰는 걸 선호하는데 문제 조건이 1-index로 주어지다 보니 풀이 글을 쓸 때 설명하기 애매한 부분이 많다... 혹 읽으면서 혼란스러우셨다면 심심한 사과의 말씀드린다.
'Algorithm > 문제 풀이' 카테고리의 다른 글
| BOJ 11726 - 2 x n 타일링 (0) | 2024.06.17 |
|---|---|
| BOJ 11834 - 홀짝 (0) | 2024.06.09 |
| BOJ 10868 - 최솟값 (0) | 2024.06.04 |
| BOJ 3080 - 아름다운 이름 [Java / Python] (0) | 2024.06.02 |
| BOJ 12015 - 가장 긴 증가하는 부분 수열 2 (0) | 2024.05.27 |



