Merge Sort
분할 정복(Divide and Conquer)
배열을 좌/우로 반씩 나눠가면서 최소 단위까지 내려간다. 이후 올라오면서 각 단위를 병합(merge)하면서 정렬하는 방식이다. 재귀로 구현하는 게 일반적이며, 각 단위를 절반씩 나누며 내려가기 때문에 재귀 깊이는 \( \log n \)이 되고, 각 깊이마다 전체 엘리먼트를 순회하며 병합하므로 \( O(n) \)의 시간복잡도가 발생한다. 모든 정렬을 수행했을 때 항상 \( O(n \log n) \) 의 시간복잡도를 보장받는다.
안정 정렬(Stable Sort)
정렬 과정에서 같은 우선순위를 가진 데이터가 정렬 후에도 순서가 유지되는 것을 안정적(Stable)이라고 표현한다. 분할 과정에서 데이터는 정렬되지 않은 상태이므로 원래 위치를 유지하고, 병합 과정에서도 우선순위가 같다면 순서가 먼저였던 데이터를 먼저 배치함으로써 Stable 상태를 유지할 수 있다.
과정
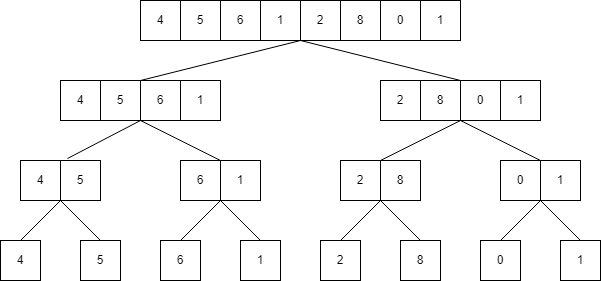
초기 배열을 [ 4, 5, 6, 1, 2, 8, 0, 1 ]로 정의하고 정렬하는 과정을 살펴보려 한다. 먼저 배열을 반씩 잘라가며 최소 단위까지 내려갈 것이다. 실제 코드는 재귀로 구현하기 때문에 첨부할 이미지와 실행 과정이 다소 차이가 있으나, 이해를 편하기 위해 각 깊이 별로 정렬 과정을 표현했다.
분할(Divide)
배열을 반씩 나눠서 하나의 엘리먼트만 남을 때까지 반복한다.
병합(Merge)
병합 과정에서 값을 비교하고 정렬을 수행한다.

왼쪽부터 차례로 n개의 엘리먼트를 순회한다. 먼저 4와 5를 병합하는 과정이다. 좌/우로 나눠서 값을 비교하고 작은 값을 먼저 채운다. 4가 더 작은 값이므로 배열의 첫 칸에 4를 채워준다.

왼쪽 배열에 남은 엘리먼트가 없으므로 5를 채워준다.

이어서 6과 1을 병합한다. 먼저 작은 값인 1이 채워지고

후에 큰 값인 6이 뒤에 채워진다

같은 과정을 반복하면 위 그림과 같아진다.

정렬된 배열을 다시 좌/우로 나누어 병합한다. 이때 양쪽 배열은 이미 정렬되어있는 상태이므로 모든 요소를 비교하는 게 아니라 아직 정렬되지 않은 요소들 중 가장 앞의 값을 비교하게 된다. 따라서 4와 1 중 작은 값인 1이 먼저 채워지고, 오른쪽 배열의 다음 비교 요소는 6이 된다. 실제 구현은 조금 다르겠지만, 일단은 오른쪽 배열의 index가 0이었다가 1로 넘어갔다고 생각해도 좋다.

정렬되지 않은 요소 [4,5]와 [6] 중 작은 값은 4가 채워진다.

남은 5와 6중 작은 값인 5가 채워지고

왼쪽에 비교할 값이 없으므로 오른쪽의 남은 엘리먼트가 채워지며 하나의 합병이 끝난다.

반대쪽까지 같은 과정을 반복하면 위와 같다. 여기까지 왔으면 마지막 부분 또한 어떻게 진행될지 그려지리라 생각한다. 그러나 안정 정렬의 특징을 보여주기 위해 몇 단계만 더 진행해 보려 한다.

다시 양쪽 배열의 첫 번째 엘리먼트를 비교한다. 0과 1중 더 작은 값인 0이 채워진다.

이제 왼쪽의 1과 오른쪽의 1을 비교하는데 왼쪽의 1이 먼저 채워진다. 이는 같은 값이라면 기존 배열에서의 순서를 지키는 안정된 상태를 유지하게 해준다. 필자는 실제 구현에서 이 부분에 대한 실수를 했었다. 아래 구현 코드에서 어떤 부분인지 주석으로 표시한다.

남은 1이 채워지고 다시 병합 과정을 반복하면

배열이 오름차순으로 정렬된다. 위에서 그림으로 표현하지 못해 텍스트로 표현한 게 하나 있는데, 만약 양쪽 배열을 비교하는 과정에서 한쪽 배열을 모두 사용하게 된다면, 남은 한 쪽 배열은 비교 없이 순서대로 채워주면 된다. 분할 후 병합해서 올라가는 과정에서 이미 정렬을 수행한 상태이므로 남은 엘리먼트는 자동으로 채울 수 있다.
구현
근래에 알고리즘 문제 풀이를 python으로 하고 있어서 고민을 좀 했는데, 아무래도 최근에 재귀 깊이 제한에 시달렸다 보니 Java로 구현하게 되었다.
package solution.implement_sort;
public class MergeSort {
// 외부에서 호출되는 메서드
public void sort(int[] arr) {
mergeSort(arr);
}
// 최초 호출
// 배열을 입력 받고, 정렬에 임시로 사용할 sorted배열을 선언해서 넘겨준다
private void mergeSort(int[] arr) {
int[] sorted = new int[arr.length];
mergeSort(0, arr.length - 1, sorted, arr);
}
// 인자로 좌/우 범위의 인덱스를 받는다
// 매 비교마다 배열을 생성한다면 메모리 할당을 계속해서 해야한다
// 파라미터로 받아온 sorted배열에 각 인덱스를 통해 값을 저장한다
private void mergeSort(int left, int right, int[] sorted, int[] arr) {
// 좌, 우 값이 같다면 값이 하나만 있으므로 return
if (left == right) {
return;
}
// 중간 값을 구하고
int mid = (left + right) / 2;
// 양쪽으로 나눠서 재귀 호출
mergeSort(left, mid, sorted, arr);
mergeSort(mid + 1, right, sorted, arr);
// 양쪽 배열 병합
merge(left, right, sorted, arr);
}
// 역시 좌/우 값을 파라미터로 받는다
private void merge(int left, int right, int[] sorted, int[] arr) {
// 저장용 배열의 인덱스. 가장 왼쪽 값부터 시작
int index = left;
// 왼쪽은 시작점부터
int l = left;
int mid = (left + right) / 2;
// 오른쪽 배열은 중간값 + 1부터 시작
int r = mid + 1;
// 양쪽 배열 중 한쪽의 모든 값을 다 사용할 때까지
while (l <= mid && r <= right) {
// 왼쪽이 오른쪽 보다 작거나 같다면 왼쪽 값을 임시 배열에 삽입한다.
// 만약 <=이 아닌 <를 사용한다면 뒷 순서의 값이 앞쪽으로 삽입되므로 stable한 상태가 깨지게 된다.
if (arr[l] <= arr[r]) {
sorted[index] = arr[l];
l++;
} else {
sorted[index] = arr[r];
r++;
}
index++;
}
// 한쪽 배열 다 채운 뒤, 남은 값을 끝까지 채워준다
if (l <= mid) {
while (index <= right) {
sorted[index] = arr[l];
index++;
l++;
}
} else {
while (index <= right) {
sorted[index++] = arr[r++];
}
}
// 주어진 구간의 값을 정렬해서 교체하는 과정
// 임시 배열의 값을 원본 배열로 복사해준다
for (int i = left; i <= right; i++) {
arr[i] = sorted[i];
}
}
}
오랜만에 구현하려다 보니 애를 좀 먹었다. Counting Sort까지 총 2개의 알고리즘을 정리하려고 했는데 오늘은 시간이 부족하지 싶다. 읽은 누군가에게 조금이라도 도움이 됐길 바라면서 포스팅을 마친다 부족한 포스팅 읽어주셨음에 감사드린다.